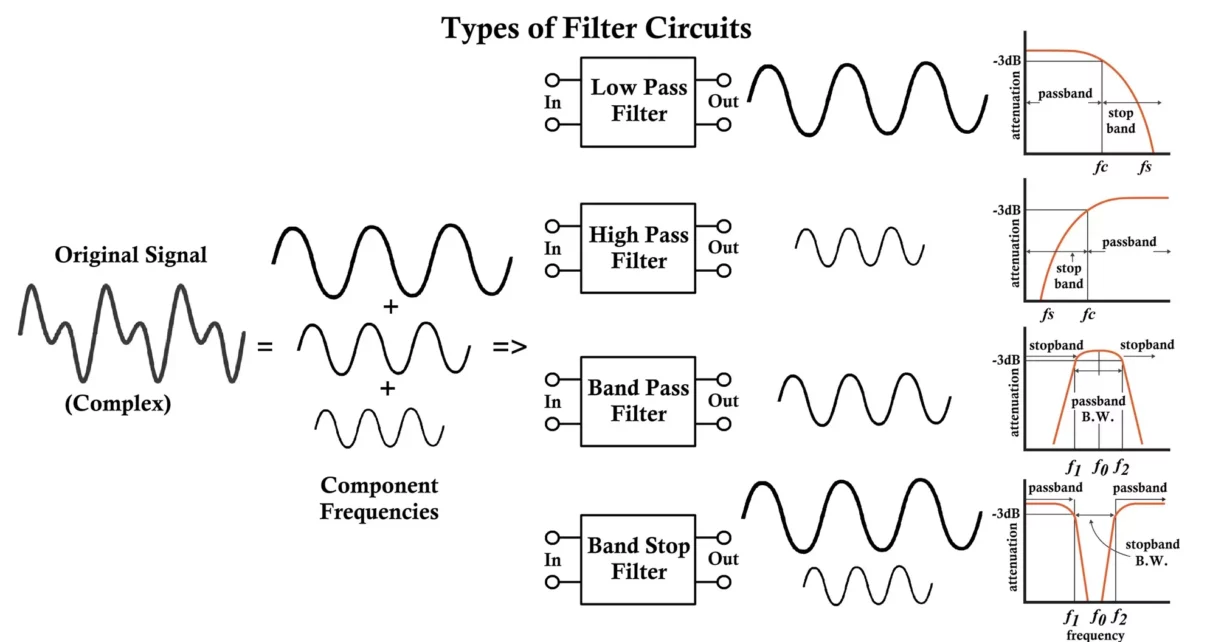
In this article, we will delve into the types of filter circuits, their working principles, essential characteristics, and common applications. Filters are indispensable components in electronics and communication systems, selectively allowing specific frequencies to pass while attenuating others. These devices or circuits shape the characteristics of signals for numerous applications like audio processing, telecommunications, and medical instrumentation.
Introduction to Filters:
A filter is a circuit designed to pass signals within a certain frequency range while attenuating signals outside that range. Depending on the design, filters can be passive (using resistors, capacitors, and inductors) or active (using operational amplifiers along with passive components). Filters are critical in removing noise, separating signals, and shaping waveforms in communication, control systems, and audio electronics.
Common Terminology in Filters:
Before diving into types of filter circuits, understanding some essential terms is crucial:
1. Passband
The passband is the frequency range where the filter allows signals to pass with little to no attenuation. For example, a low-pass filter has a passband for all frequencies below its cutoff frequency.
2. Stopband
The stopband defines the range of frequencies where the filter significantly attenuates the signal. These are the frequencies that the filter is designed to block.
3. Cut-off Frequency (fC)
It is the frequency at which the output of a filter is reduced by -3 dB from the maximum gain. In the case of low-pass filters, the cut-off frequency is the highest frequency that can pass through the filter. Conversely, in high-pass filters, it is the lowest frequency that can pass.
4. -3 dB Frequency (f3dB)
- The -3 dB frequency, often referred to as the cut-off frequency, is the frequency at which the output power of a system falls to half of its maximum value. In terms of voltage, this corresponds to a reduction in voltage to approximately 70.7% of its maximum value.
- This frequency is significant in characterizing the bandwidth of a system. For a filter, it defines the boundary between passband and stopband.
5. Upper and Lower Cut-off Frequencies
-
- Lower Cut-off Frequency (fL): This is the frequency below which signals are attenuated. Frequencies above this threshold can pass through the filter. The lower cutoff frequency marks the lower end of the passband or stopband.
- Upper Cut-off Frequency (fH): This is the frequency above which signals are also attenuated. Frequencies below this threshold can pass. The upper cutoff frequency defines the upper limit of the passband or stopband.
The range between the lower and upper cut-off frequencies defines the passband of the filter.
6. Center Frequency (f₀)
In band-pass and band-reject filters, the center frequency is the frequency at which the filter’s response is most pronounced—either passing or rejecting the signal.
7. Bandwidth (B.W.)
Bandwidth is the range between the lower and upper cutoff frequencies, indicating how wide the passband or stopband is. A wider bandwidth allows more frequencies to pass (in a band-pass filter) or be rejected (in a band-reject filter).
8. Roll-Off Rate
This term refers to how quickly the filter attenuates the signal beyond the cutoff frequency. It is expressed in decibels per octave (dB/octave) or decibels per decade (dB/decade).
- For a low-pass filter with a -3 dB frequency of 1 kHz, signals below 1 kHz pass with minimal attenuation, while signals above 1 kHz are significantly attenuated.
- For a band-pass filter with a lower cut-off frequency of 200 Hz and an upper cut-off frequency of 2 kHz, signals between these two frequencies can pass, while those outside are attenuated.
Filters are generally classified based on their construction or frequency response characteristics.
Types of Filter Circuits Based on Construction:
1. Passive Filters
Passive filters use passive components like resistors, capacitors, and inductors to filter signals. They do not require any external power and are suitable for high-frequency applications. However, they cannot provide gain and have limited flexibility in tuning compared to active filters.
Working:
- Passive filters rely on the impedance characteristics of their components to block or pass certain frequencies.
- For instance, in a low-pass passive filter, a capacitor in parallel with the load reduces high-frequency components by presenting a low impedance path, effectively “shorting” them to ground.
Applications:
- Radio Frequency (RF) Communication: For selecting or rejecting certain signal frequencies.
- Power Supply Smoothing: To reduce ripple in DC power supplies.
2. Active Filters
Active filters include active components like operational amplifiers (op-amps) along with resistors and capacitors. These filters can provide signal amplification (gain) and offer more control over frequency response characteristics, making them suitable for low-frequency applications.
Working:
- Active filters use op-amps to buffer the signal and control the gain. By combining feedback from the op-amp with resistor-capacitor (RC) networks, these filters allow more precise tuning of the cutoff frequency.
- In a low-pass active filter, for example, the RC network sets the cutoff frequency, while the op-amp amplifies the output signal.
Applications:
- Audio Processing: Equalizers and tone controls in audio systems.
- Signal Conditioning: In instrumentation to amplify and filter out noise.
Types of Filter Circuits Based on Frequency Response:
1. Low-Pass Filter (LPF)
A low-pass filter (LPF) allows frequencies below a certain cutoff to pass while attenuating higher frequencies. These filters are essential in audio electronics, communications, and signal processing.
Working:
- In a passive low-pass filter, a resistor and capacitor are connected in series. The capacitor blocks high-frequency signals by presenting lower impedance to them, while the resistor allows low-frequency signals to pass.
- In an active LPF, an op-amp controls the cutoff frequency and gain while the RC network filters high-frequency noise.

Cutoff frequency for RC low-pass filter:
fc = 1 / (2πRC)
Transfer function (voltage gain):
H(s) = 1 / (1 + sRC)
Attenuation and Gain:
The voltage gain H(f) at frequency f is given by:
H(f) = 1 / √(1 + (f / fc)2)
Applications:
- Audio Systems: To block high-frequency noise, ensuring smooth audio output.
- Smoothing Circuits: To remove high-frequency components from signals in digital-to-analog converters.
2. High-Pass Filter (HPF)
A high-pass filter (HPF) works oppositely to a low-pass filter, allowing frequencies higher than the cutoff frequency to pass and attenuating lower frequencies. HPFs are used to block DC components and low-frequency noise.
Working:
- In a passive HPF, a capacitor and resistor are connected in series, but the capacitor is now in front of the load. The capacitor allows high frequencies to pass but blocks low frequencies due to higher impedance at lower frequencies.
- In an active HPF, an op-amp amplifies the signal while the RC network filters out low frequencies.

Cutoff frequency for RC high-pass filter:
fc = 1 / (2πRC)
Transfer function:
H(s) = (sRC) / (1 + sRC)
Attenuation and Gain:
The voltage gain at frequency f is:
H(f) = (f / fc) / √(1 + (f / fc)2)
Applications:
- DC Blocking: Removing DC components from AC signals in instrumentation.
- Telecommunications: Filtering out low-frequency interference in transmission lines.
3. Band-Pass Filter (BPF)
A band-pass filter (BPF) allows signals within a specific frequency range to pass while attenuating signals outside that range. It is a combination of both high-pass and low-pass filters.
Working:
- In a BPF, the circuit combines a low-pass and high-pass filter in series, creating a passband between the two cutoff frequencies.
- Active band-pass filters often use op-amps to maintain signal strength while filtering out unwanted frequencies outside the passband.

Resonant frequency for an RLC band-pass filter:
f0 = 1 / (2π√(LC))
Bandwidth (BW):
BW = fH - fL = R / L
Quality Factor (Q-factor):
Q = f0 / BW = f0 L / R
Attenuation and Gain:
The transfer function of an RLC band-pass filter:
H(s) = (sL) / (R + sL + (1 / sC))
Applications:
- Radio Communication: Selecting the desired frequency band while rejecting others.
- Audio Equalizers: Enhancing specific frequency bands in music production.
4. Band-Stop/Reject Filter (Notch Filter)
A band-reject filter, also known as a notch filter, attenuates a specific range of frequencies while allowing frequencies outside this range to pass. Notch filters are useful in eliminating unwanted frequencies like power line noise.
Working:
- A band-reject filter is created by placing a band-pass filter in parallel with the signal path. The filter attenuates a narrow frequency range, effectively “notching” out a specific frequency.
- In active designs, the op-amp provides greater precision in defining the width and depth of the notch.

Resonant frequency for an RLC band-stop filter:
f0 = 1 / (2π√(LC))
Bandwidth (BW):
BW = R / L
Quality Factor (Q-factor):
Q = f0 L / R
Attenuation and Gain:
The transfer function of an RLC band-stop filter:
H(s) = (R + sL + (1 / sC)) / (R + sL)
Applications:
- Noise Reduction: Removing specific interference like the 60 Hz hum from power lines.
- Instrumentation: Eliminating narrowband noise in measurement systems.
5. All-Pass Filter
An all-pass filter allows all frequencies to pass through but changes the phase relationship between different frequencies. This makes it ideal for phase correction.
Working:
- All-pass filters use RC networks and op-amps to alter the phase without affecting the amplitude of the signal. The phase shift can be controlled by the components’ values.
Applications:
- Phase Shifters: Used in control systems and audio processing to align phase differences.
- Signal Processing: Correcting phase in systems where timing is critical.
Bode Plots (General Formula)
Bode plots are used to represent the frequency response (magnitude and phase) of filter circuits.
The transfer function H(f) is typically a complex number that can be written in the form:
H(f) = Re(H(f)) + j ⋅ Im(H(f))
- Re(H(f)) is the real part of the transfer function.
- Im(H(f)) is the imaginary part of the transfer function.
- j is the imaginary unit, where j² = -1.
Formula for gain in decibels (dB)
Magnitude (gain) in dB:
GdB = 20 log10(|H(f)|)
Phase response:
θ(f) = tan-1(Im(H(f)) / Re(H(f)))
General Transfer Function for a Filter
In general, the transfer function H(s) of a filter relates the output to the input in the s-domain, where s = jω. The general form for any filter can be expressed as:
H(s) = N(s) / D(s)
Where N(s) is the numerator polynomial in s, and D(s) is the denominator polynomial in s.
Key Formulas of all Four Types of Filter Circuits:
| Filter Type | Formula for Cutoff/Resonant Frequency | Transfer Function |
|---|---|---|
| Low-Pass | fc = 1 / 2πRC | H(s) = 1 / (1 + sRC) |
| High-Pass | fc = 1 / 2πRC | H(s) = (sRC) / (1 + sRC) |
| Band-Pass | f0 = 1 / 2π√(LC) | H(s) = (sL) / (R + sL + (1 / sC)) |
| Band-Stop | f0 = 1 / 2π√(LC) | H(s) = (R + sL + (1 / sC)) / (R + sL) |
Applications of Filter Circuits in Various Domains:
Varius types of filter circuits are used in many practical applications across different fields:
- Audio Processing: In audio system filters like low-pass and high-pass eliminate noise and shape sound, while band-pass filters are used in equalizers to control specific frequencies.
- Communication Systems: Band-pass and notch filters help tune specific frequencies, remove interference, and improve signal quality in radio, TV, and telecommunication systems.
- Power Supplies: Low-pass filters smooth out output voltage by filtering noise in AC-to-DC converters, and EMI filters block unwanted electromagnetic interference.
- Medical Devices: Filters in ECG and EEG devices remove noise for cleaner signal readings, while band-pass filters in ultrasound equipment enhance imaging quality.
- Signal Conditioning: Filters clean up sensor signals by eliminating unwanted noise before analog-to-digital conversion in precision systems.
- RF and Microwave Communication: Filters select desired frequency bands for wireless communication, rejecting interference in systems like cell phones and satellite communication.
- Instrumentation: Low-pass filters remove high-frequency noise for accurate measurements, and all-pass filters correct phase distortions in precise timing systems.
- Radar and Sonar: Band-pass filters isolate target signals in radar and sonar systems, improving detection accuracy.
- Image Processing: High-pass filters sharpen images by enhancing edges, while low-pass filters reduce noise.
- Control Systems: Low-pass filters smooth control signals in industrial automation, while notch filters eliminate oscillation-causing frequencies.
- Consumer Electronics: Filters in TVs, radios, and smartphones manage broadcast and communication bands to reduce interference.
- Digital Signal Processing (DSP): FIR and IIR digital filters are used in communication, audio, and image processing to remove noise and enhance signals.
Conclusion:
Filters are vital components in modern electronics, with applications ranging from audio processing to RF communication and power management. By understanding how passive filters, active filters, low-pass filters, high-pass filters, band-pass filters, and band-reject filters work, you can design systems that meet specific signal processing requirements. There are filters like Butterworth filter, Chebyshev filter and many other types of filter circuits, you can study them for more details. The right choice of filter depends on the desired frequency response, the type of components available, and the intended application, making it an essential area of study in both analog and digital electronics.
Types of Diodes with Symbol, Definition, Working and Applications