While a BCD adder performs decimal addition using binary hardware with correction logic, a BCD subtractor performs the subtraction of one BCD number from another and produces a valid BCD result. This requires additional logic because simple binary subtraction does not automatically produce valid BCD outputs.
Digital systems frequently need to perform arithmetic operations such as addition and subtraction on decimal numbers. Since digital circuits operate internally in binary form, decimal numbers must be represented in a binary-compatible format. One of the most widely used representations is Binary Coded Decimal (BCD), where each decimal digit (0 to 9) is represented by a unique 4-bit binary code.
What is a BCD Subtractor?
A BCD Subtractor is a digital circuit that subtracts one BCD digit from another and produces a valid BCD output along with borrow information if required.
Mathematical representation
- A = Minuend (BCD digit)
- B = Subtrahend (BCD digit)
Then the circuit computes:
Difference = A - B
If A ≥ B, the result is a valid positive BCD digit (0 to 9).
If A < B, a borrow is generated and correction is applied.
Need for BCD Subtractor
Binary subtractors can subtract binary numbers correctly, but their outputs may not correspond to valid BCD digits (0000 to 1001). Values like 1010 (10) to 1111 (15) are invalid in BCD.
Hence, a BCD subtractor:
- Performs binary subtraction
- Detects invalid BCD results
- Applies correction to convert the result into a valid BCD digit
Principle of Operation
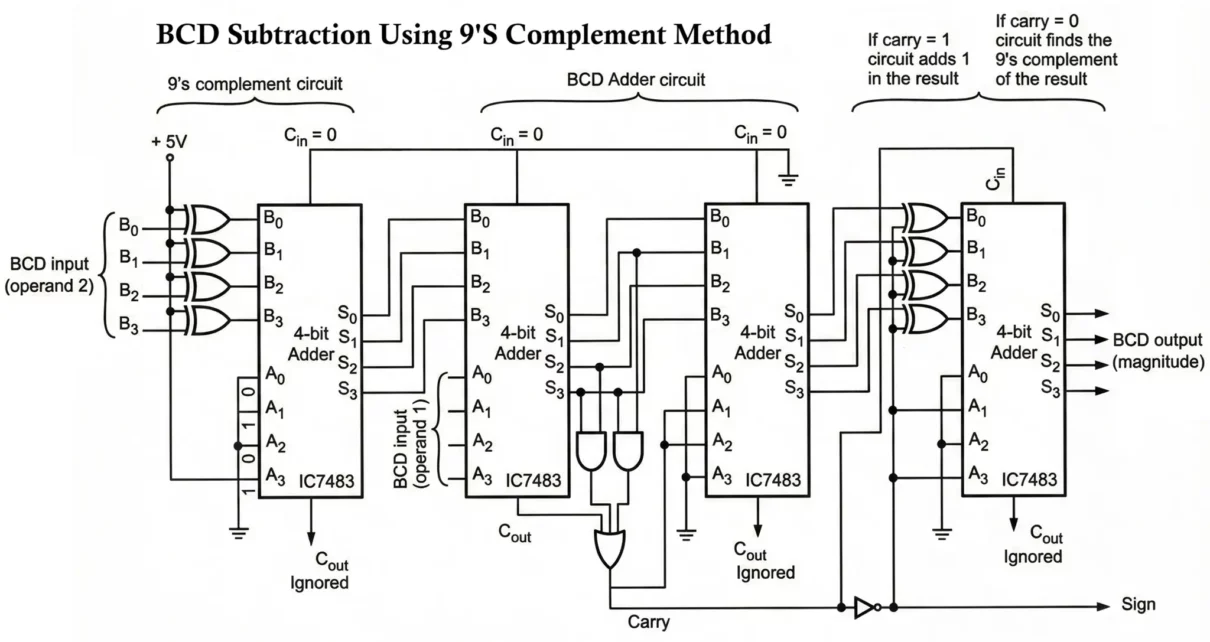
The BCD subtraction is generally implemented using the 9’s complement method (or equivalently 10’s complement).
- Take the 9’s complement of the subtrahend B.
- Add it to the minuend A using a BCD adder.
- If there is a carry, discard it and the result is positive.
- If there is no carry, take the 9’s complement of the sum and attach a negative sign.
Why Complement Methods Are Used?
Direct subtraction in BCD is difficult because:
- BCD is not a pure binary system (only 0000–1001 are valid).
- Binary subtraction may produce invalid BCD codes.
To simplify hardware, subtraction is converted into addition by using:
- 9’s complement (for decimal / BCD)
- 10’s complement (9’s complement + 1)
This allows reuse of the BCD adder.
Complement Definitions
For a decimal digit d:
| Method | Complement |
|---|---|
| 9’s complement | 9 − d |
| 10’s complement | 10 − d = (9 − d) + 1 |
In BCD logic, 9’s complement is easier to implement and widely used.
BCD Subtractor Circuit Diagram

The circuit is composed of:
- A 9’s complement generator for B
- A BCD adder made up of two IC7483 4bit binary adder
- Correction logic
- Carry / borrow detection
Truth Table for BCD Subtraction
| A (Decimal) | B (Decimal) | Binary A | Binary B | A − B | Result (BCD) | Borrow |
|---|---|---|---|---|---|---|
| 5 | 3 | 0101 | 0011 | 2 | 0010 | 0 |
| 7 | 4 | 0111 | 0100 | 3 | 0011 | 0 |
| 4 | 6 | 0100 | 0110 | −2 | 0010 | 1 |
| 9 | 9 | 1001 | 1001 | 0 | 0000 | 0 |
| 2 | 5 | 0010 | 0101 | −3 | 0011 | 1 |
Borrow = 1 indicates negative result.
Correction Logic
After binary subtraction, the result may be invalid BCD. A correction of +6 (0110) is applied when:
- There is a borrow, or
- The binary result exceeds 1001.
This ensures that the final output lies between 0000 and 1001.
BCD Subtractor Example
Example: 7 − 4
- A = 7 → 0111
- B = 4 → 0100
- 9’s complement of B = 5 → 0101
- Add: 0111 + 0101 = 1100
- Since carry is present, discard carry and correct result → 0011 (3)
Example: 4 − 6
- A = 4 → 0100
- B = 6 → 0110
- 9’s complement of B = 3 → 0011
- Add: 0100 + 0011 = 0111 (no carry)
- Take 9’s complement of 0111 → 0010 (2) and borrow = 1 → result = −2
BCD subtraction using 10’s complement
BCD arithmetic subtraction by adding the 10’s complement of the subtrahend to the minuend.

The circuit is composed of:
- A 10’s complement generator for B
- A BCD adder made up of two IC7483 4bit binary adder
- Correction logic
- Carry / borrow detection
10’s complement method:
To compute A – B
- Find the 9’s complement of B: (9 – B)
- Add 1 to get the 10’s complement: (10 – B)
- Add this to A: A + (10 – B)
- If there is a carry out, discard the carry → result is positive.
- If there is no carry, take the 10’s complement of the sum and prefix a minus sign → result is negative.
In a BCD subtractor, this is implemented with:
- A BCD adder,
- A 9’s complement generator for the subtrahend digit,
- An initial carry-in = 1 (to form 10’s complement),
- BCD correction logic (add 0110 if the sum exceeds 9).
Example: 7 – 4
Step 1 Find 10’s complement of 4
- 10 – 4 = 6
- In BCD: 4 = 0100
- 9’s complement = 1001 − 0100 = 0101 (which is 5)
- +1 → 0110 (which is 6)
Step 2 Add to the minuend
- 7 + 6 = 13
- In BCD: 7 = 0111, 6 = 0110
Binary addition:
0111 + 0110 ------ 1101
1101 = 13 in decimal.
Since this is greater than 9, BCD correction is required:
Add 0110:
1101 + 0110 ------ 1 0011
This gives: Carry = 1 and
Step 3 Interpret the carry
- Carry exists → discard it.
- Result = 0011 (which is 3)
- So, the final result is: 7 – 4 = 3
This illustrates how a BCD subtractor uses the 10’s complement of the subtrahend and a BCD adder to perform subtraction using only addition hardware.
Advantages of BCD Subtractor
- Compatible with decimal systems
Operates directly on decimal digits encoded in BCD, making it ideal for financial, commercial, and human-interface systems where decimal accuracy is required. - Avoids binary-to-decimal conversion
No need to convert BCD to binary and back, which reduces conversion hardware and rounding errors. - Simple hardware reuse
Uses a standard BCD adder plus complement logic, so subtraction is implemented using addition circuitry. - Exact decimal arithmetic
Prevents floating-point rounding errors common in binary representations of decimal fractions. - Easy cascading for multi-digit subtraction
Each digit stage is identical, making it modular and scalable.
Disadvantages of BCD Subtractor
- More hardware than binary subtractors
Requires:- Complement generation,
- Initial carry insertion,
- BCD correction logic (add 6 when >9),
leading to more gates than pure binary subtraction.
- Slower operation
Extra correction and carry propagation increase propagation delay. - Inefficient bit usage
BCD uses 4 bits per digit but only 10 of 16 codes are valid, wasting encoding space. - Higher power consumption
Due to increased logic and switching activity. - Complex negative result handling
Requires detecting carry and sometimes re-complementing the result.
Applications of BCD Subtractor
- Financial and accounting systems
Used where exact decimal subtraction is mandatory (banking, billing, taxation). - Digital calculators
Performs decimal subtraction on display digits. - Embedded systems with numeric displays
Systems that process and display decimal values directly (e.g., weighing scales, meters). - Industrial instrumentation
Measurement and control systems using decimal setpoints and readings. - Point-of-sale (POS) and commercial devices
Price calculations, receipts, and transaction systems. - Time and date arithmetic
In clocks, counters, and scheduling hardware using decimal digits.
Conclusion
The BCD subtractor is an essential building block in digital systems that process decimal numbers rather than pure binary data. By combining complement arithmetic, BCD addition, and correction logic, it ensures accurate and valid decimal subtraction suitable for human-readable digital outputs. Though slightly more complex than binary subtractors, its role in calculators, measurement instruments, and financial electronics makes it indispensable.
BCD Adder Circuit Diagram, Truth Table, Working and Applications
Seven Segment Display: Types, Working, Pin Diagram & Applications
Analog to Digital Converter (ADC) Block Diagram, Working, Types & Applications